对光的解释，有射线光、波动光、量子光几类解释，分别对应用到几何光学，物理光学，量子力学领域知识。
什么是波？不仅仅是软绵绵、圆鼓鼓的那个，物理学中的波是一种随时间推移，在空间内发生转移的能量。
波：在空间中以特定形式传播的物理量。
答案是显而易见的————时间停转，水止风静，同样的，时间静止的时候，波一定也是停止传播的；那么，波的传播的另一个条件，就应当是随着时间的推移，也就是波的传播是与时间和空间都有联系的，波向前运动时，时间增加，走过的路径也同时增加。
所以说，波的传播与时间有关，通常包含时间参量 $t$。
那么，我们就可以根据这一定义，发现一些波的例子，比如:
一般形式的光波：
| 时间域 | 空间域 | |
|---|---|---|
| 周期 | $T$ | $\lambda$ |
| 频率 | $v$ | $f$ |
| 角频率 | $\omega=2\pi v=\frac{2\pi}{T}$ | $k=2 \pi f = \frac{2\pi}{\lambda}$ |
e光：由于波矢动量守恒，所以其等相位面依然与入射等相位面一致，只是
#------------------------#
# 限制层 $n_1$ #
# 波导层 $n_1$ #
# 限制层 $n_2$ #
#------------------------#
作用：可以在两个方向上都控制住光的折射损耗。
$n_1>n_2, n_1>n_3$
通常：波导一定是在折射率最大的层中传播的，否则损耗非常大。
结构：
应用：
| 射线光学 | 波动光学 | |
|---|---|---|
| 适用条件 | $\lambda « d$ | $\lambda ~ d$ |
| 研究对象 | 光线 | 模式 |
| 基本方程 | 射线方程 | 波导场方程 |
| 研究方法 | 折射、反射定理 | 边值问题 |
| 主要特点 | 约束光线 | 模式 |
用不同的坐标系，可以得到不同的边界条件的，更复杂的解。
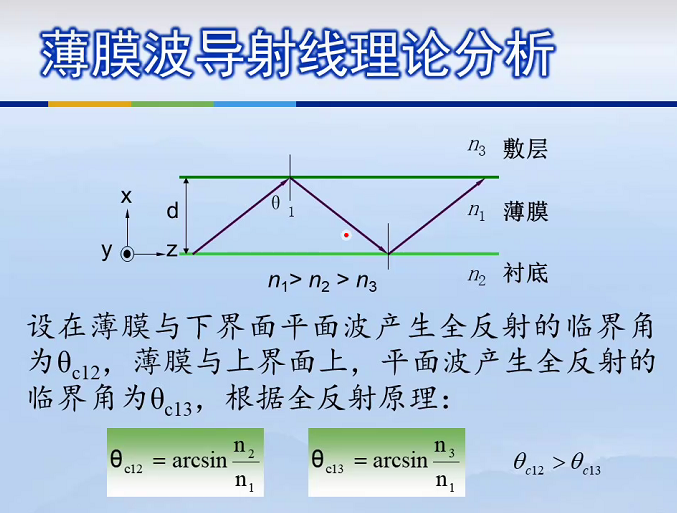
如果只停留在全反射层面，说明你的波导理论还没有入门？ 实际传输的不是一根光线，而是一束等相位光场传播，当发生反射时，空间局部会发生交叠。 平面光束越宽，交叠区域越大 -> 引发一个核心问题：输出为若干光场的叠加，薄膜光场输出为一个干涉光场。
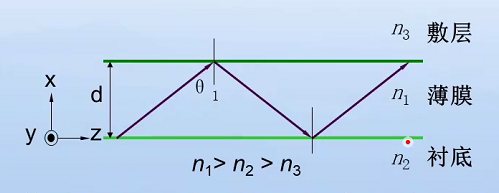两者虽然可以由相同的（波矢）等相位面方向，但是其位相会发生偏移。两者在空间中叠加时，传输方向相同，同频率，等相位面相同，可产生干涉。
波矢在两次反射中上下两次
局域场中的普适结论：
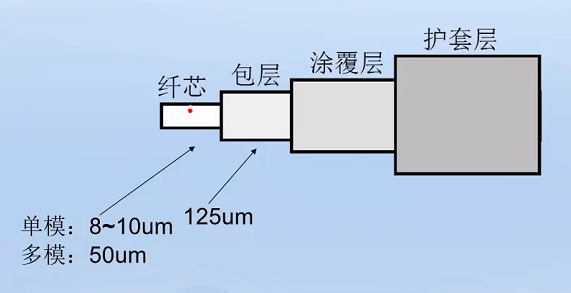
分阶跃型光纤、梯度折射率光纤。
通信常用：阶跃型单模光纤。
对称型平板波导，其TE、TM模式同时存在、且无法区分，所以可以认为是单个模式，即单模光纤。
对应临界折射角，存在一个临界入射角 $\varphi$， 则数值孔径：
物理意义：表示光纤捕捉光线的能力，NA越大，捕获能力越强。
对于 $\lambda = 1.55\mu m$ 处典型值 $$
不考。
当 $n_1,\ n_2$ 都很小时，可以近似为
数值孔径：与纤芯与包层的折射率差（又与$\Delta$有关）有关。
光栅：广义来讲，具有周期性
单缝衍射因子：当缝宽很宽，（~1cm时），由于缝宽远大于波长，所以衍射效应不明显，多缝干涉的前提是，单缝衍射效应要足够明显。
超人 两个的折射率不同，光程差公式可以省略那部分的影响吗 东篱悠然 进入房间
黄礼刚 相邻光束的传播距离非常近，所以不同光束之间的相位差主要由衍射角度决定，而不是由声光效应带来的额外差 黄礼刚 所以布拉格光栅主要是振幅效应，拉曼奈斯衍射主要是相位效应