【数学】现代工程学数学基础

极限与连续

微分

多元函数微分法

积分

反常积分

信号与系统、傅里叶变换中常用的无穷积分： $\begin{aligned} \mathscr{F}\left\{ 1 \right\} &= \int_{-\infty}^{\infty} 1 \cdot e^{-jwt}dt \\ &= -\frac{1}{jw}e^{-jwt} \Big| ^{t=\infty} _{t=-\infty} \end{aligned}$

向量微分

复变函数

线性代数

无穷级数

泰勒级数

数学中，泰勒级数用于展开任意函数，常用于复杂函数的近似计算，如正弦函数 $y(x) = \sin x$，由英国数学家布鲁克·泰勒（Sir Brook Taylor）于1715年发表.

• 在自变量零点处求得的泰勒级数又称麦克劳林级数，以英格兰数学家柯林·麦克劳林的名字命名。
• 泰勒级数在近似计算中有着广泛应用。
• 在复变函数的求解中，也常常用到泰勒展开的几种常用形式。

$$\begin{aligned} f(x) &= \sum_{n=0} ^{\infty} \frac{f^{(n)}(x_0)}{n!}\left(x-x_0\right)^n \\ &= f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)(x-x_0)^2}{2!}+...+ \frac{f^{(n)}(x_0)(x-x_0)^n}{n!}+... \end{aligned}$$

• $f(x) = \sqrt{1+x}$ $\begin{aligned} f(x) &= f(0) + f'(0)(x-0) + \frac{f^{(2)}(x_0)x^2}+\frac{f^{(3)}x^3}{3!}+... \\ &= \sqrt{1+0} + \left(\frac{1}{2}\frac{(1+0)^{-\frac{1}{2}}}{1!}x\right) + \left( -\frac{1}{4}\frac{(1+0)^{-\frac{3}{2}}}{2!} x^2\right) + \left( \frac{3}{8} \frac{(1+0)^{-\frac{5}{2}}}{3!}x^3 \right) +... \\ &= 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16}x^3+... \end{aligned}$
• $y = \sin x$

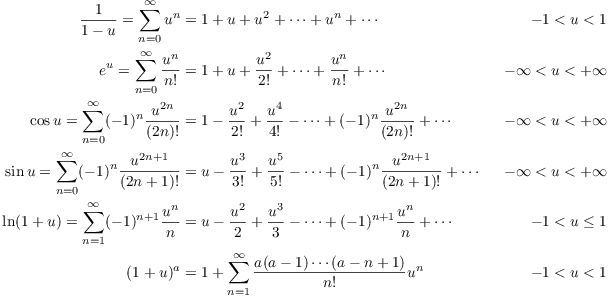
傅里叶级数

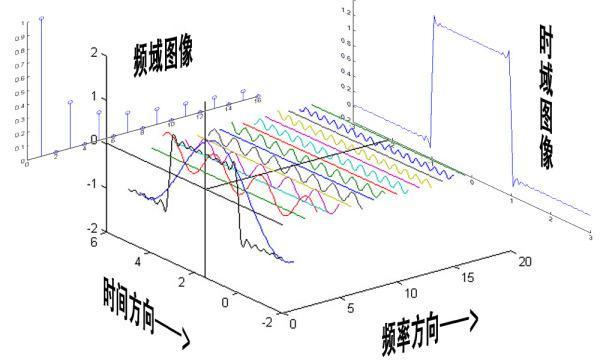
傅里叶变换对

傅里叶变换： $\begin{aligned} \mathscr{F} \left\{ f(t) \right \} &= \int_{-\infty} ^{\infty} f(t) \cdot e^{-jwt} \mathrm{d}t \\ &= \int_{-\infty} ^{\infty} f(t) \cdot e^{-j2\pi wt} \mathrm{d}t \\ &= F(jw) \\ &= F(j 2 \pi f) \end{aligned}$

傅里叶反变换： $\begin{aligned} \mathscr {F^{-1}} \left\{ F(jw) \right\} &= \int_{-\infty} ^{\infty} F(jw) \cdot e^{jwt} \mathrm{d}w \\ \end{aligned}$

常用的傅里叶变换对

原函数	傅里叶变换	备注
$1$	$2\pi\delta(jw)$
$\delta(t)$	$1$

• $\boxed{1\ \ \text{»}\ \ 2\pi\delta(jw)}$
  通常由 $(2)$ 式反推 $(1)$ 式，$\delta(t)$ 的傅里叶变换是 $1$，所以 $F(jw) = 1$ 的傅里叶反变换是 $\delta(t)$，即$\frac{1}{2 \pi}\int_{-\infty}^{\infty} 1 \cdot e^{jwt} dw = \delta(t)$，又由积分的对称性（从$-\infty$到$\infty$），所以对 $e^{jwt}$ 积分与 对$e^{-jwt}$ 积分并没有数值上的区别，所以$\int_{-\infty}^{\infty}1 \cdot e^{-jwt}dt = 2\pi \delta(jw)$。
  • $$\tag{1} \begin{aligned} \int_{-\infty}^{\infty}1 \cdot e^{-jwt}dt &= \int_{-\infty}^{0} e^{-jwt}dt + \int_{0}^{\infty}e^{-jwt}dt \\ &= -\frac{1}{jw}e^{-jwt}\Big|_{-\infty}^{0}+ -\frac{1}{jw}e^{-jwt}\Big|^{\infty}_0 \\ &= 2\pi\delta(jw) \end{aligned}$$
  • $$\tag{2} \frac{1}{2\pi}\int_{-\infty}^{\infty} \delta(jw) \cdot e^{jwt}dw = \frac{1}{2\pi}$$
• $\boxed{\delta(t)\ \ \text{»}\ \ 1}$
  • $$\tag{3} \int_{-\infty}^{\infty} \delta(t)\cdot e^{-jwt}dt = 1$$
  • $$\tag{4} \frac{1}{2 \pi}\int_{-\infty}^{\infty} 1 \cdot e^{jwt} dw = \delta(t)$$

FAQ

1. 为什么用 $jw$ 作为傅里叶变换表达式的自变量而不是 $w$？

傅里叶变换

拉普拉斯变换